$$\newcommand{\TM}{(Q,\Gamma, \Sigma, \delta, q_0, q_{accept}, q_{reject})}$$

Chuch-Turing-Tesen

Læringsmål

• Forstå ækvivalensen mellem de udvidede turing-maskin-modeller og den oprindelige Turing-maskin-model
• Forstå Church-Turing-tesen og hvad dens forudsætninger er.
• Forstå at der er en dualitet mellem beslutningsproblemer og medlemskab af sprog
• Andvende dualiteten mellem beslutningsproblemer og sprog til at oversætte instanser af det ene begreb til instanser af det andet.
• Forstå strengbeskrivelses-notation og dens rolle og kunne anvende den til at oversætte beslutningsproblemer til sprog.

Flere Bånd?

Overføringsfunktion: $$ \delta: Q \times \Gamma^k \longrightarrow Q \times (\Gamma \times {L,R})^k $$

Simulering af en k-bånds TM med ét Bånd

Prikkerne markerer læsehovedets placering

$$\Gamma_{\text{ny}} = \Gamma \cup \{\dot{a} \mid a \in \Gamma\} \cup \{\#\}$$

Simulering af et skridt:

1. Scan den ikke-blanke del af båndet, og find ud af hvad prikkerne peger på (Husk det vhja. tilstand)
2. Flytte prikker og erstat tegn sådan som k-bånds-maskinen ville kræve det.
   • Skub indhold mod højre, om nødvendigt

Sætning

Hvis et sprog $L$ kan genkendes af en k-bånds-TM, kan $L$ også genkendes af en 1-bånds-TM.

• Flere bånd betyder ikke noget for regnekraft!

Nondeterminisme

$$DFA \sim NFA\\ DPDA \nsim PDA\\ \scriptstyle (DPDA \to PDA)\\ \scriptstyle (DPDA \nleftarrow PDA)\\ $$

$$TM \sim NTM$$

Overføringsfunktion for NTM: $$ \delta : Q \times \Gamma \longrightarrow \mathcal{P}(Q \times \Gamma) $$

Eksempel

$$ \delta(q_8, a)={(q_9,b,R),(q_7, a,R)} $$

Accept

Definition

En NTM $M$ accepterer en streng, hvis der i beregningstræet for strengen forekommer en konfiguration hvis tilstand er $q_{accept}$

Simulering af NTM

Sker ved at gennemvandre beregningstræet og lede efter en accepterende konfiguration

Problem: NTM'er kan gå i uendelig løkke, så grene i træet KAN være uendeligt lange!

Løsning:

Idé: Brug breddesøgning

På input $w$

1. Kopier $w$ over på bånd 1
2. For $k=0,1,2,...$
   1. Kopier input fra bånd 1 til bånd 2
   2. Generer næste indexfølge af længde $k$
   3. Simuler en beregning på bånd 2 svarende til indexfølgen på bånd 3
   4. Hvis beregningen besøger $q_{accept}$: accepter!

Sætning

Hvis $L$ kan genkendes af en NTM, kan $L$ genkendes af en TM!

• Vigtigt af flere grunde:
  • Nondeterminisme giver ikke øget regnekraft
  • Vi må godt gøre brug af nondeterminisme!

Enumerator

TM'er som sproggenkendere:

$$L_{input}(M)=\{ w \in \Sigma^* \mid M\ \text{accepterer}\ w \}0$$

TM'er som sproggeneratorer (enumerator):

$$L_{output}(M)=\{ w \in \Gamma^* \mid M\ \text{udskriver}\ w\ \text{på tomt input} \}$$

Sætning

$L$ er et genkendeligt

​ $\Updownarrow$

$\exists$ enumerator $E$ så $E$ outputter $L$ ($L_{output}(E)=L$)

Se bevis i Lektion 2, afsnit 4

Andre Modeller for Beregnelighed

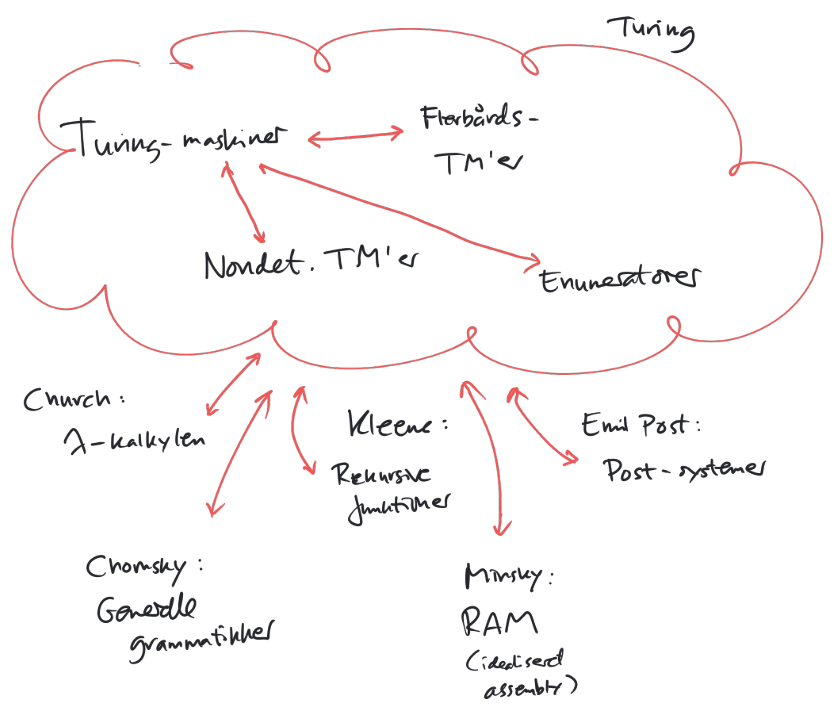
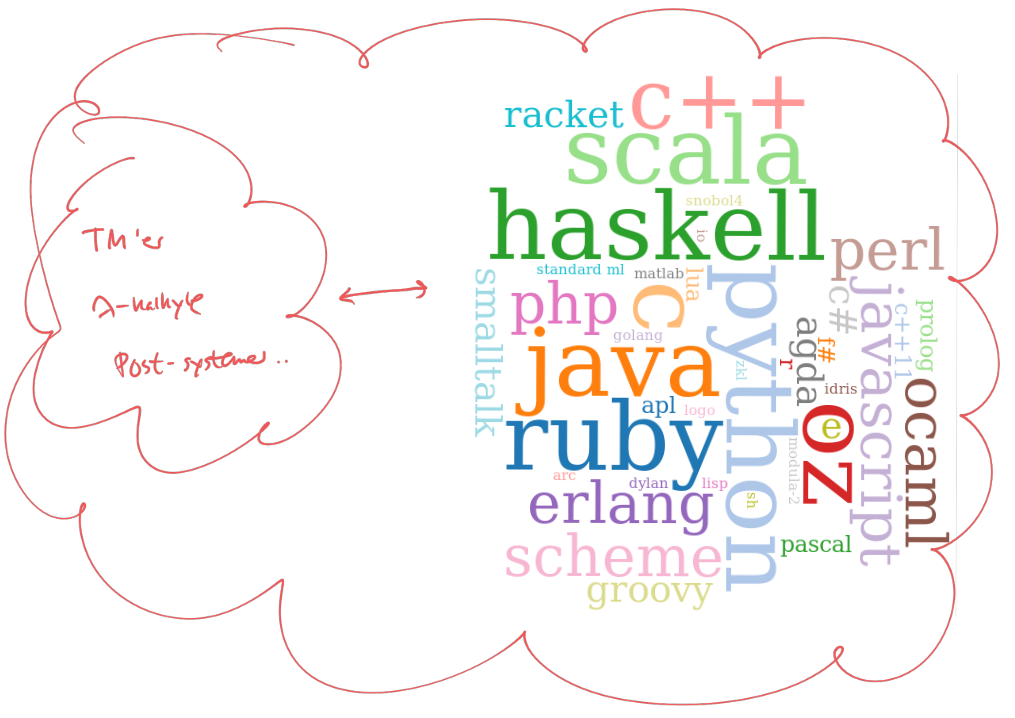
Alle modeller for beregnelighed vi kender i dag, er højest lige så stærke som Turing Maskiner.

• Inklusive programmeringssprog

Church-Turing-tesen

Enhver model for beregnelighed vil være højest lige så stærk som TM-modellen, hvis ellers den er rimelig.

• Kan ikke bevises (ikke en matematisk sætning)
  • Kan potentielt modbevises.

Konsekvenser

• Alle varianter af TM'er er nyttige, når vi skal vise at et sprog er genkendeligt
• Pseudokode er nok til at beskrive en TM's adfærd

Beslutningsproblemer og Sprog

Beslutningsproblemer:

• Ja-nej-spørgsmål
  • Eksempler:
  • Givet en graf G, er G sammenhængende?
  • Givet et tal n, er n et primtal?
  • Givet en TM M og et input w, vil M acceptere w?

De understregede elementer er parametre / input i problemet.

Sprog $\leftrightarrow$ Beslutningsproblem

Et hvert beslutningsproblem kan formuleres som et sprog. Og til hvert sprog er der et beslutningsproblem:

• Givet $w$, er $w\in L$?

Eksempel

"Givet $G$, er $G$ da en sammenhængende graf?"

$<G>$: Strengrepræsentationen af $G$

Problem svarer til: $$ CONN={\ \mid G\ \text{er en sammenhængende graf}} $$

Altså

Et beslutningsproblem kan afgøres med en algoritme hvis, det tilsvarende sprog er afgørbart!

---

Last update: September 15, 2019